MAT101 Graded Exam 4
Question 1
Identify the asymptotes.
f (x) = −2×2+5x−4x+3−2×2+5x−4x+3
Select one:
a.Horizontal asymptote: x = 0
Vertical asymptote: x = 3
b.Horizontal asymptote: x = 0
Slant asymptote: y = -2x + 11
c.Vertical asymptote: x = -3
d.Vertical asymptote: x = -3
Slant asymptote: y = -2x + 11
Correct Answer Question 1
d.Vertical asymptote: x = -3
Slant asymptote: y = -2x + 11

Question 2
Graph the function.
f (x) = −4x2x2+4−4x2x2+4
Select one:
a.
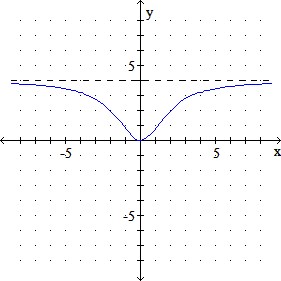
b.
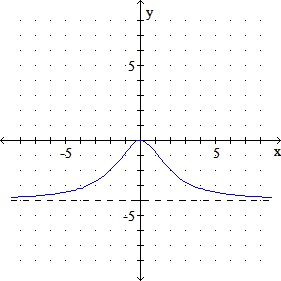
c.
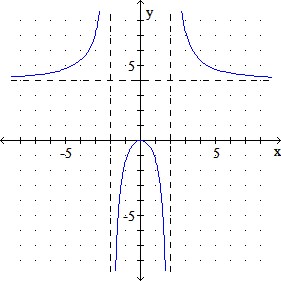
d.
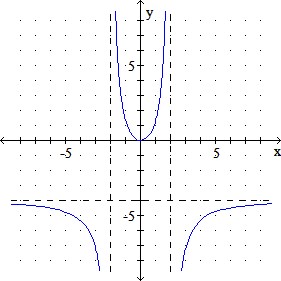
Correct Answer Question 2
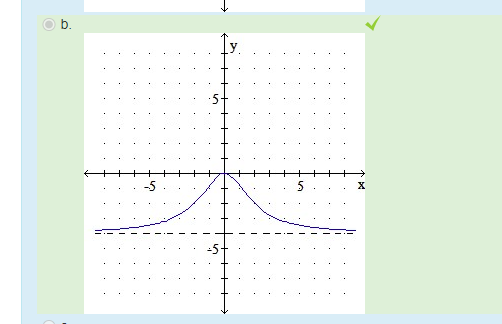
Question 3
A power company burns coal to generate electricity. The cost C(x) (in $1000) to remove x% of the air pollutants is given by
C¯¯¯¯(x)=800×100−xC¯(x)=800×100−x.
If the power company budgets $1.2 million for pollution control, what percentage of the air pollutants can be removed? Round to two decimal places, if necessary.
Select one:
a.60%
b.0.15%
c.0.6%
d.14.98%
Correct Answer Question 3
60%

To get all solutions to MAT101 Graded Exam 4 – Solving Linear Systems Using Augmented Matrices
…Please click on the Icon below to purchase the FULL QUIZ ANSWERS at only $7
Question 4
Solve the inequality. Write the solution set in interval notation.
71−x≤23−x71−x≤23−x
Select one:
a.(1, 3)
b.(−∞,195](−∞,195]
c.(1, 3) U [195,∞)[195,∞)
d.(-∞, 1) U (3, ∞)
Question 5
The graph of y = f (x) is given. Solve the inequality.
f (x) ≤ 0
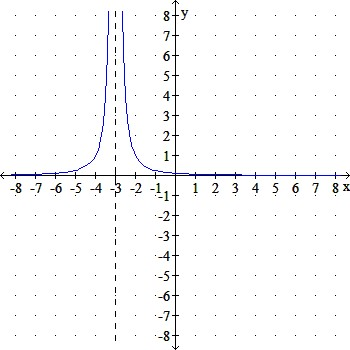
Select one:
a.{-3}
b.(-∞, ∞)
c.(-∞, -3] U [-3, ∞)
d.{ }
Question 6
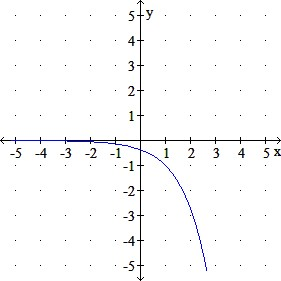
Use transformations of the graph y = ex to graph the function. Write the domain and range in interval notation.
f (x) = –ex + 1
Select one:
a.
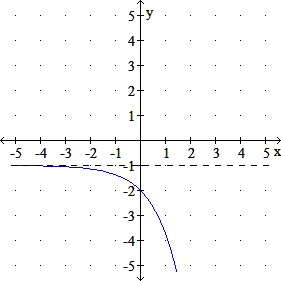
Domain: (-∞, ∞)
Range: (-∞, -1)
b.
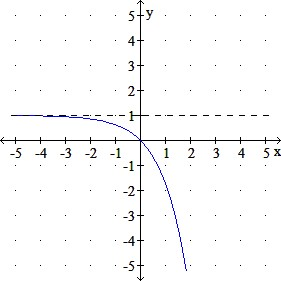
c.
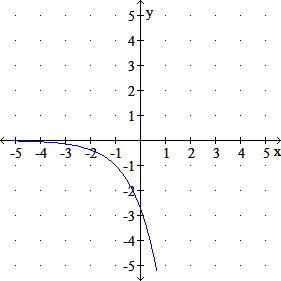
d.
Question 7
Solve the problem.
The level of a sound in decibels is calculated using the formula
D = 10 ∙ log(I × 1012)
where I is the intensity of the sound waves in watts per square meter. A electric shaver puts out 0.0001 watt per square meter. How many decibels is that?
Select one:
a.800
b.-40
c.8
d.80
Question 8
Write the logarithmic expression as a single logarithm with coefficient 1, and simplify as much as possible.
5logb y + 3logb z
Select one:
a.logb (y5z3)
b.8 logb (y + z)
c.logb (y5 + z3)
d.15 logb (yz)
Question 9
Solve the equation. Write the solution set with the exact values given in terms of natural or common logarithms. Also give approximate solutions to 4 decimal places, if necessary.
55x + 6 = 48x ; use natural logarithms
Select one:
a.
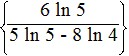
; x ≈ -3.1732
b.
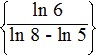
; x ≈ 3.8122
c.
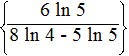
; x ≈ 3.1732
d.{ }
Question 10
The sales of a book tend to increase over the short-term as word-of-mouth makes the book “catch on.” The number of books sold N(t) for a new novel t weeks after release at a certain book store is given in the table for the first 6 weeks.
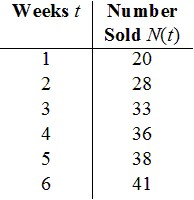
Book Sales vs. Weeks After Release
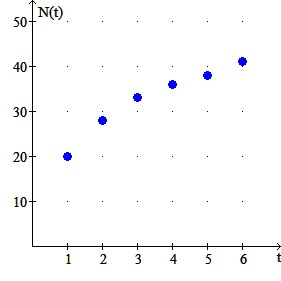
Week
a. Find a model of the form y = a + b ln t.
b. Use the model to predict the sales in week 11. Round to the nearest whole unit.
c. Is it reasonable to assume that the logarithmic trend will continue? Why or why not?
Select one:
a. a.y = 20.1 + 11.5 ln t
b. 48 books
c. No. The trend cannot continue indefinitely. At some point, book sales will begin to decrease as most reading enthusiasts have read the book.
b.a.y = 3.9 + 19 ln t
b. 49 books
c. No. The trend cannot continue indefinitely. At some point, book sales will begin to decrease as most reading enthusiasts have read the book.
c. a.y = 3.9 + 19 ln t
b. 49 books
c. Yes. The number of books sold will continue to increase although the sales will approach a limit.
d. a.y = 20.1 + 11.5 ln t
b. 48 books
c. Yes. The number of books sold will continue to increase although the sales will approach a limit.
Question 11
Solve the system by using any method. If a system does not have one unique solution, state whether the system is inconsistent or whether the equations are dependent.
y = 7878x + 3
8y – 7x = 24
Select one:
a.{(x,y) | y = 7878x + 3}; The equations are dependent.
b.{3737,278278}
c.{ }; The system is inconsistent.
d.{(0, 3)}
Question 12
Solve the problem.
Nail polish remover is essentially a mixture of water and a chemical called acetone. How much pure acetone must be combined with a solution that is 28% acetone to make 24 oz of a 58% solution?
Select one:
a.14 oz
b.10 oz
c.17 oz
d.12 oz
Question 13
Solve the problem.
A helicopter flies 168 miles against the wind in 2 hours; with the wind, it can fly 252 miles in the same amount of time. Find the speed of the helicopter in still air.
Select one:
a.63 miles per hour
b.21 miles per hour
c.105 miles per hour
d.84 miles per hour
Question 14
Determine if the ordered triple is a solution to the system of equations.
−4x+8y+2z=−40−4x+8y+2z=−40
−9x+8y+8z=−27−9x+8y+8z=−27; ( -4, -6, -1)
−8x+6y−8z=14−8x+6y−8z=14
Select one:
a. No
b. Yes
Question 15
Solve the system. If a system has one unique solution, write the solution set. Otherwise, determine the number of solutions to the system, and determine whether the system is inconsistent, or the equations are dependent.
−9x−6z=19−9x−6z=19
y+8z=−2y+8z=−2
x−3y=35x−3y=35
Select one:
a.{(0, -18, 16)}
b.{(−199,2,0)}{(−199,2,0)}
c.{(−3,2,43)}{(−3,2,43)}
d.{(−3,−383,43,)}{(−3,−383,43,)}
Question 16
Perform the indicated row operations, then write the new matrix.
Select one:
a.
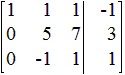
b.
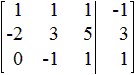
c.
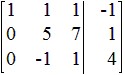
d.
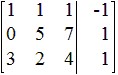
Question 17
Use a calculator to approximate the reduced row-echelon form of the augmented matrix representing the given system. Give the solution set where x, y, and z are rounded to 2 decimal places.
0.52x-3.79y-4.67z=9.15
0.03x+0.06y+0.13z=0.53
0.974x+0.813y+0.419z=0.189
Select one:
a.{(-4.49, -6.63, 2.49)}
b.{(6.18, -11.2, 7.82)}
c.{(-15.61, -1.39, -2.84)}
d.{(7.91, -1.03, 3.18)}
Question 18
Write a system of linear equations represented by the augmented matrix.

Select one:
a. x = -7
y = 9
z = – 1919
b. x = 7
y = -9
z = 1919
c. x = 7
y = 9
z = 1919
d. x = -7
y = -9
z = 1919
Question 19
Solve the system using Gaussian elimination or Gauss-Jordan elimination.
-4x – 6y + 5z = 13
8x + 4y – 7z = -7
4x – 2y – 2z = -15
Select one:
a.{ }
b.{(8, 4, 5)}
c.{(8, 5, 4)}
d.{(5, 8, 4)}
Question 20
Solve the system using Gaussian elimination or Gauss-Jordan elimination.
-2x – y + 3z = 13
x – 3y – 3z = -4
Select one:
a.{(1, 2, -3)}
b.{ }
c.{(127127z – 437437, – 3737z – 5757, z) | z is any real number}
d.{(-1, -2, 3)}
To get all solutions to MAT101 Graded Exam 4 – Solving Linear Systems Using Augmented Matrices
Related: [FULL COURSE] MAT101 College Algebra
…Please click on the Icon below to purchase the FULL QUIZ ANSWERS at only $7




