MAT101 Graded Exam 3 Graphing Polynomial Functions
Question 1
Find the exact distance between the points.
(5–√5, −3–√−3) and (45–√45, −73–√−73)
Select one:
a. 3√17
b. 6√7
c.2√42
d.2√58
Correct Answer Question 1
a. 3√17

Question 2
Determine whether the relation defines y as a function of x.
Select one:
a.Function
b.Not a function
Correct Answer Question 2
a. Function

Question 3
Determine the slope of the line passing through the given points.
(311−−√11, 66–√6) and (11−−√11, 6–√6)
Select one:
a.m = (5√66)/22
b.m = – 2
c.m = 2
d.m = −(5√66)/22
Correct Answer Question 3
m = (5√66)/22

To get all 100% correct solutions for MAT101 College Algebra Graded Exam 3
…Please click on the Icon below to purchase the FULL ANSWER at only $7
Question 4
Use the graph to solve the equation and inequality. Write the solution to the inequality in interval notation.
a. 3x – 3 = 2x – 1
b. 3x – 3 > 2x – 1
Select one:
a.a. {3}; b. (3, ∞)
b.a. {3} b. (-∞, 3}
c.a. {2}; b. (-∞, 2)
d.a. {2}; b. (2, ∞)
Question 5
Determine if the lines defined by the given equations are parallel, perpendicular, or neither.
y = 7575x – 2
y = – 7575x – 4
Select one:
a.neither
b.perpendicular
c.parallel
Question 6
Use transformations to graph the given function.
q(x) = 5x−−√5x
Select one:
a.
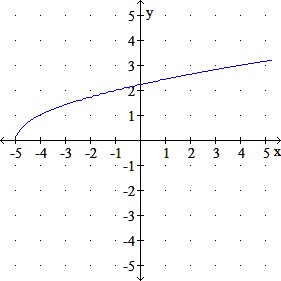
b.
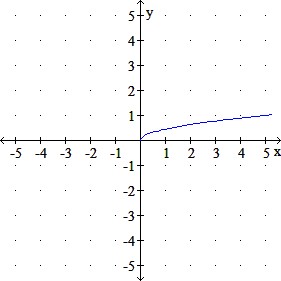
c.
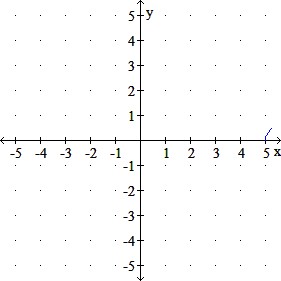
d.
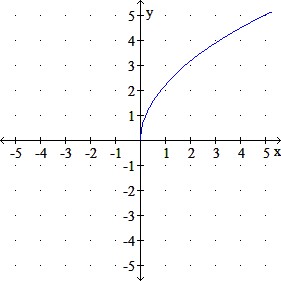
Question 7
The graph of y = f (x) is given. Graph the indicated function.
Graphy = f (-x) – 4

Select one:
a.
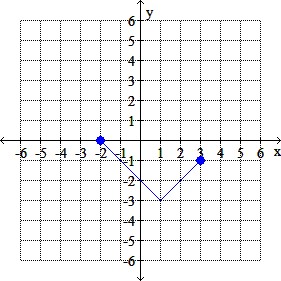
b.
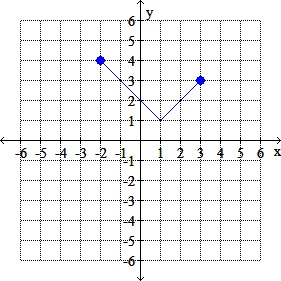
c.

d.
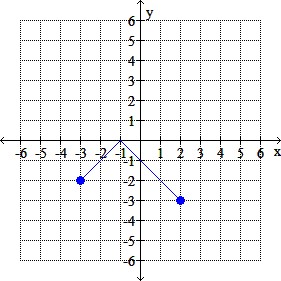
Question 8
Use interval notation to write the intervals over which f is and
Select one:
a.a. (-∞, -2) (2, ∞)
b. never decreasing
c. (-2, 2)
b.a. (-4, ∞)
b. (-∞, -4)
c. never constant
c.a. never increasing
b. (-∞, -2) (2, ∞)
c. (-2, 2)
d.a. (-∞, 2) (2, ∞)
b. never decreasing
c. (-2, 2)
Question 9
Determine the minimum or maximum value of the function.
k(x) = 3x2 – 4x
Select one:
a.Maximum: 4343
b.Minimum: – 4343
c.Minimum: 4343
d.Maximum: – 4343
Question 10
Graph the function and determine the minimum or maximum value of the function.
m(x) = – 1414(x + 1)2
Select one:
a.maximum value = 0
b.minimum value = 0
c.maximum value = 0
d.minimum value = 0
Question 11
p  = 3
= 3 3 – 3
3 – 3
a. Identify the power function of the form y = x n that is the parent function to the given graph.
b. In order, outline the transformations that would be required on the graph of y = x n to make the graph of the given function.
c. Match the function with the graph.
i.
ii.
iii.
iv.
Select one:
a.a.y = x3
b. Shift y = x3 to the left 3 units. Shrink vertically by a factor of . Shift downward 3 units.
c.Graph iv.
b.a.y = x3
b. Shift y = x3 to the left 3 units. Stretch vertically by a factor of 3. Shift downward 3 units.
c.Graph i.
c.a.y = x3
b. Shift y = x3 to the left 3 units. Stretch vertically by a factor of 3. Shift downward 3 units.
c.Graph ii.
d.a.y = x3
b. Shift y = x3 to the left 3 units. Stretch vertically by a factor of 3. Shift downward 3 units.
c.Graph iii.
Question 12
Solve the problem.
f = –
4
a. Identify the power function of the form y = xn that is the parent function to the given graph.
b. In order, outline the transformations that would be required on the graph of y = xn to make the graph of the given function.
c. Match the function with the graph.
i.ii.
iii.iv.
Select one:
a.a.y = x4
b. Shift y = x4 to the right 1 units. Shrink vertically by a factor of . Reflect across the x-axis.
c.Graph ii.
b.a.y = x4
b. Shift y = x4 to the left 1 units. Shrink vertically by a factor of . Reflect across the x-axis.
c.Graph iii.
c.a.y = x4
b. Shift y = x4 to the left 1 units. Shrink vertically by a factor of .
c.Graph i.
d.a.y = x4
b. Shift y = x4 to the right 1 units. Shrink vertically by a factor of . Reflect across the x-axis.
c.Graph iii.
Question 13
Write a polynomial f (x) that meets the given conditions. Answers may vary.
Degree 3 polynomial with zeros 4, 5i, and -5i
Select one:
a.f (x) = x3 – 4x2 – 25x + 100
b.f (x) = x3 + 4x2 – 25x – 100
c.f (x) = x3 + 4x2 + 25x + 100
d.f (x) = x3 – 4x2 + 25x – 100
Question 14
Use synthetic division to divide the polynomials.
(s4 + 5s3 + 2s2 – 17s + 7) ÷ (s – 1)
Select one:
a.s3 + 6s2 + 8s – 9
b.s3 + 4s2 – 2s – 15 + 22s+122s+1
c.s3 + 6s2 + 8s + −9s+2s−1−9s+2s−1
d.s3 + 6s2 + 8s – 9 – 2s−12s−1
Question 15
Find all the zeros.
f (x) = x3 + 10x2 + 25x + 18
Select one:
a.2, -4 ± 7–√7
b.-2, -4 ± 7–√7
c.-2, -4 ± 7i
d.2, -4 ± 7i
Question 16
Find the zeros and their multiplicities. Consider using Descartes’ rule of signs and the upper and lower bound theorem to limit your search for rational zeros.
f (x) = x9 + 10x8 + 27x7 + 20x6 + 50x5
Select one:
a.0 (multiplicity 5), -5 (multiplicity 2) and ±i2–√2 (each multiplicity 1)
b.0 (multiplicity 5), 5 (multiplicity 2) and ±i2–√2 (each multiplicity 1)
c.0 (multiplicity 5), 5 (multiplicity 2) and ±2i (each multiplicity 1)
d.0 (multiplicity 5), 5 (multiplicity 2) and ±2–√2 (each multiplicity 1)
Question 17
A one-to-one function is given. Write an expression for the inverse function.
g (x) = r (x + q)7 + s
Select one:
a.g -1(x) =
b.g -1(x) = – q
c.g -1(x) =
d.g -1(x) = – q
Question 18
Provide the missing information.
Given the function f : = {(1, 2), (2, 3), (3, 4)} write the set of ordered pairs representing f -1
(please use the same format in your answer including commas between ordered pairs)
Correct Answer Question 18
Question 19
A one-to-one function is given. Write an expression for the inverse function.
f (x) =
Select one:
a.f -1(x) = 6 – 2x
b.f -1(x) =
c.f -1(x) = 6 + 2x
d.f -1(x) =
Question 20
The graph of a function is given. Graph the inverse function.
Select one:
a.
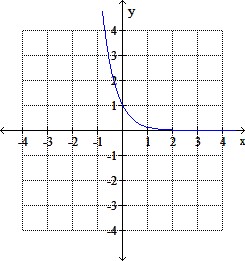
b.
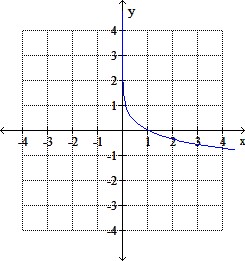
c.
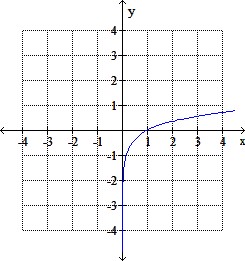
d.
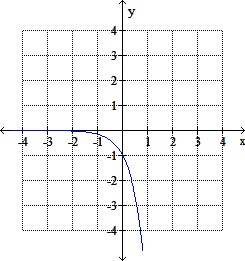
Related: (Solution) MAT101 Graded Exam 4 – Solving Linear Systems
To get all 100% correct solutions for MAT101 College Algebra Graded Exam 3
…Please click on the Icon below to purchase the FULL ANSWER at only $7




