MAT101 Graded Exam 2
Solve the rational equation.

Solve for the indicated variable.
L = 1/3πq2s for s

Question 3
In the mid-nineteenth century, explorers used the boiling point of water to estimate altitude. The boiling temperature of water T (in °F) can be approximated by the model T = -1.83a + 212, where a is the altitude in thousands of feet. Determine the temperature at which water boils at an altitude of 9,000 ft. Round to the nearest degree.
The Correct Answer is 196 °F
To determine the temperature at which water boils at an altitude of 9,000 feet, the given formula is:
T=−1.83a+212
where T is the temperature in °F and a is the altitude in thousands of feet. Since the altitude is 9,000 feet, we can set a=9 (because 9,000 feet is 9 thousand feet).
Now, substitute a=9 into the formula:T=−1.83(9)+212
T=−16.47+212
T=195.53
Question 4
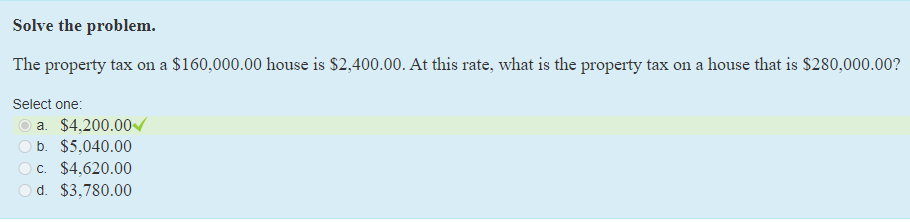
The property tax on a $160,000.00 house is $2,400.00. At this rate, what is the property tax on a house that is $280,000.00?
Correct Answer 4,200
We have all the correct answers to MAT101 Graded Exam 2
…Please click on the Icon below to purchase the FULL QUIZ ANSWERS at only $7
Two cars are 261 miles apart and travel toward each other on the same road. They meet in 3 hours. One car travels 3 mph faster than the other. What is the average speed of each car?
Select one:
a.42 mph; 45 mph
b.41 mph; 44 mph
c.39 mph; 42 mph
d.40 mph; 43 mph
Question 6
Correct
Mark 8.75 out of 8.75
Question text
Solve the problem.
Suppose that a merchant buys a patio set from the wholesaler for $260. At what price should the merchant mark the patio set so that it may be offered at a discount of 25% but still give the merchant a 20% profit on his $260 investment?
Select one:
a.$325
b.$416
c.$312
d.$377
Question 7
Correct
Mark 8.75 out of 8.75
Question text
Perform the indicated operation. Write the answer in the form a + bi.
(6 + −9−−−√−9)(8 – −9−−−√−9)
Select one:
a.
57 – 2i9–√9
b.39
c.39 + 2i9–√9
d.57 + 2i9–√9
Question 8
Correct
Mark 8.75 out of 8.75
Question text
Perform the indicated operation. Write the answer in the form a + bi.
(-5 – 9i)(6 + 6i)
Select one:
a.-84 – 84i
b.24 – 84i
c.24
d.-30 – 54i
Question 9
Correct
Mark 8.75 out of 8.75
Question text
Perform the indicated operation. Write the answer in the form a + bi.
7i(-5 + 5i)
Select one:
a.35 – 35i
b.-30i
c.-35 – 35i
d.-70i
Question 10
Correct
Mark 8.75 out of 8.75
Question text
Solve the quadratic equation by completing the square and applying the square root property.
n2 + 18n = -75
Select one:
a.{-9 – 249−−−√249, -9 + 249−−−√249}
b.{−18−249√2,−18+249√2}{−18−2492,−18+2492}
c.{-9 – 6–√6, -9 + 6–√6}
d.{9 – 6–√6, 9 + 6–√6}
Question 11
Correct
Mark 8.75 out of 8.75
Question text
Solve the equation by using the quadratic formula.
y2 = 4y – 9
Select one:
a.{-4 ± 2i 5–√5}
b.{- 2 ± i 5–√5}
c.{4 ± 2i 5–√5}
d.{2 ± i 5–√5}
Question 12
Correct
Mark 8.75 out of 8.75
Question text
Solve the equation by using the quadratic formula.
5y – 6 + 50y2 = 0
Select one:
a.{35±2,791√5i}{35±2,7915i}
b.{13,25}{13,25}
c.{52,−103}{52,−103}
d.{−25,310}{−25,310}
Question 13
Correct
Mark 8.75 out of 8.75
Question text
Solve the problem.
A model rocket is launched from a raised platform at a speed of 176 feet per second. Its height in feet is given by
h(t) = -16t2 + 176t + 20 (t = seconds after launch).
After how many seconds does the object reach its maximum height?
Select one:
a.2.75 seconds
b.7.5 seconds
c.20 seconds
d.5.5 seconds
Question 14
Correct
Mark 8.75 out of 8.75
Question text
Solve the problem.
The width of a rectangular box is 4 in. The height is one-fifth the length x. The volume is 180in2180in2. Find the length and the height of the box.
Select one:
a.length = 4 in.; height = 20 in.
b.length = 20 in.; height = 4 in.
c.length = 3 in.; height = 15 in.
d.length = 15 in.; height = 3 in.
Question 15
Correct
Mark 8.75 out of 8.75
Question text
Solve the equation by using substitution.
(t + 3)2 – (t + 3) – 12 = 0
Select one:
a.{4, -3}
b.{1, -6}
c.{-7, 0}
d.{-1, 6}
Question 16
Correct
Mark 8.75 out of 8.75
Question text
Make an appropriate substitution and solve the equation.
(3x + 7)2 + 2(3x + 7) – 15 = 0
Select one:
a.{−23,−43}{−23,−43}
b.{−4,−43}{−4,−43}
c.{−23,−103}{−23,−103}
d.{−4,−103}{−4,−103}
Question 17
Correct
Mark 8.75 out of 8.75
Question text
Solve the equation.
100x3 + 25x2 + 4x + 1 = 0
Select one:
a.{−14}{−14}
b.{−14,±15i}{−14,±15i}
c.{−14,±15}{−14,±15}
d.{−4,±5}{−4,±5}
Question 18
Correct
Mark 8.75 out of 8.75
Question text
Solve the compound inequality. Graph the solution set, and write the solution set in interval notation.
−1≤2x+33<4−1≤2x+33<4
Select one:
a.(−3,92](−3,92]
b.(−∞,−3)(−∞,−3) U [92,∞)[92,∞)
c.(−∞,−3](−∞,−3] U (92,∞)(92,∞)
d.[−3,92)[−3,92)
Question 19
Correct
Mark 8.75 out of 8.75
Question text
Solve the inequality. Write the solution set in interval notation.
-2(4y – 7) + y ≥ 2y – (-8 + y)
Select one:
a.(34,∞)(34,∞)
b.(−∞,34)(−∞,34)
c.(−14,∞)(−14,∞)
d.(−∞,34](−∞,34]
Question 20
Correct
Mark 8.75 out of 8.75
Question text
Solve the problem.
The width of a rectangle is fixed at 30 cm, and the perimeter can be no greater than 170 cm. Find the maximum length of the rectangle.
Select one:
a.70 cm
b.55 cm
c.110 cm
d.140 cm
Related: (Solution) MAT101 Graded Exam #3 Graphing Polynomial Functions
We have all the correct answers to MAT101 Graded Exam 2
…Please click on the Icon below to purchase the FULL QUIZ ANSWERS at only $7




