BUS 5413 Analysis Assignment 4
Part 1 (23 points)
The Empirical Rule is based on the standardized normal distribution.
- Describe how you could use the Empirical Rule to evaluate the distribution of scores on a national test. You are given the following information for the national test: (1) the population mean = 450 and (2) the population SD = 75.
- Based on the information given above, estimate the range of scores on this test. That is, estimate the low score and the high score on the test. Discuss how you arrived at your estimate for each score.
- Determine where students’ test scores on the national test would place them in terms of their percentile ranking. You are given the following information on the test scores of three students.
- Student A scored a 600. What percentile is this student?
- Student B scored a 225. What percentile is this student?
- A student’s score placed them in the 99th percentile. Estimate the student’s score using whatever means gives you a good estimate.
Part 2 (20 points)
You should be familiar with the concept of using the z-formula to calculate probabilities for values that cannot be solved neatly with the Empirical Rule. The z-calculation can be used to determine the proportion of a certain salary range. The population mean for salaries was $1100, and the population standard deviation was $80. Please answer the following questions. Be sure to show your work.
- What percent of salaries range from $1100 to $1200?
- What percent of salaries are below $950?
- What percent of salaries range from $1050 to $1250?
Note 1: You must show all your work (including all calculations) step by step to earn credit. Answers alone are not sufficient. Failure to include the Excel worksheet will result in substantial penalties, more likely no credit for the assignment.
Note 2: Save your management in a Word file. The required file name standard is, LastNameFirst initial_AA1a. Example: TimmonsR_AA1b. docx. If an Excel file, example: TimmonsR_AA1a. xlsx.
Related: (Solution) BUS 5413 – Understanding Measurement Survey Methods
Solution – BUS 5413 Analysis Assignment 4
Part 1: Empirical Rule and Test Score Distribution
Using the Empirical Rule to Evaluate Test Score Distribution
The Empirical Rule applies to a normal distribution and allows us to estimate the percentage of data that falls within a certain number of standard deviations from the mean. The rule states:
- 68% of data falls within 1 standard deviation of the mean.
- 95% of data falls within 2 standard deviations of the mean.
- 99.7% of data falls within 3 standard deviations of the mean.
Given the population information for the national test:
- Mean (μ) = 450
- Standard Deviation (σ) = 75
We can now use the Empirical Rule to estimate the range of test scores.
1. Range of Scores
- Low Score: To estimate the low score, we subtract 3 standard deviations from the mean:
Low Score = μ−3σ = 450−3(75) = 450−225 = 225
- High Score: To estimate the high score, we add 3 standard deviations to the mean:
High Score = μ+3σ = 450+3(75) = 450+225 = 675
Thus, based on the Empirical Rule, 99.7% of scores will fall between 225 and 675.
2. Percentile Ranking for Students
We use the z-score formula to convert the given test scores into percentiles:
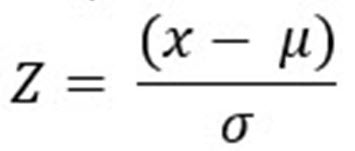
z = (X−μ)/σ
where:
σ is the standard deviation.
X is the student’s score,
μ is the mean,
Student A: Score = 600
Z = (600−450)/75 = 150/75 = 2
Using the standard normal distribution table, a z-score of 2 corresponds to approximately 97.7 percentile. Therefore, Student A is in the 97.7th percentile.
…Please click on the Icon below to purchase the full answer at only $10




