(Solution) MAT101 Graded Exam 3 Graphing Polynomial Functions

MAT101 Graded Exam 3 Graphing Polynomial Functions

Question 1

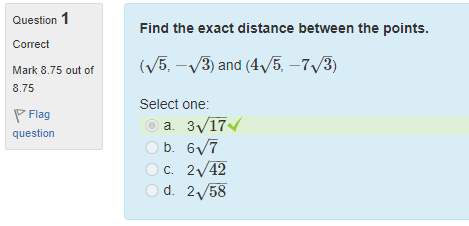
Find the exact distance between the points.

(5–√5, −3–√−3) and (45–√45, −73–√−73)

Select one:

a. 3√17

b. 6√7

c.2√42

d.2√58

Correct Answer Question 1

a. 3√17

Question 2

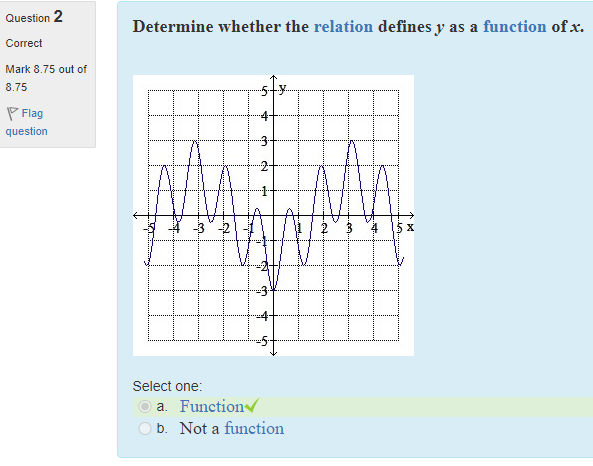
Determine whether the relation defines y as a function of x.

Select one:

a.Function

b.Not a function

Correct Answer Question 2

a. Function

Question 3

Determine the slope of the line passing through the given points.

(311−−√11, 66–√6) and (11−−√11, 6–√6) 

Select one:

a.m = (5√66)/22

b.m = – 2

c.m = 2

d.m = −(5√66)/22

Correct Answer Question 3

m = (5√66)/22

To get all 100% correct solutions for MAT101 College Algebra Graded Exam 3

…Please click on the Icon below to purchase the FULL ANSWER at only $7

Question 4

Use the graph to solve the equation and inequality. Write the solution to the inequality in interval notation.

a. 3x – 3 = 2x – 1
b. 3x – 3 > 2x – 1

Select one:

a.a. {3}; b. (3, ∞)

b.a. {3} b. (-∞, 3}

c.a. {2}; b. (-∞, 2)

d.a. {2}; b. (2, ∞)

Question 5

Determine if the lines defined by the given equations are parallel, perpendicular, or neither.

y =  7575x – 2
y = – 7575x – 4

Select one:

a.neither

b.perpendicular

c.parallel

Question 6

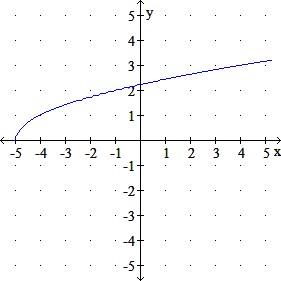
Use transformations to graph the given function.

q(x) = 5x−−√5x

Select one:

a.

b.

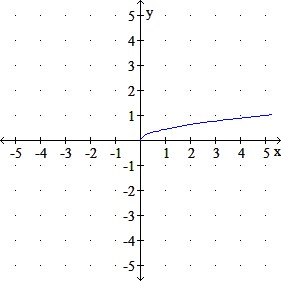
c.

d.

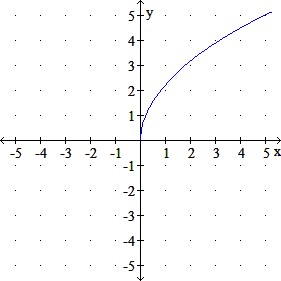
Question 7

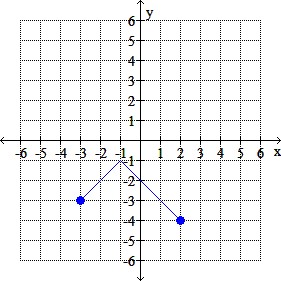
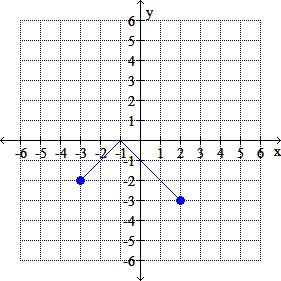
The graph of y = f (x) is given. Graph the indicated function.

Graphy = f (-x) – 4

Select one:

a.

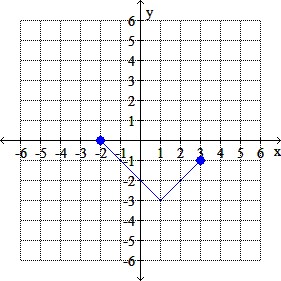
b.

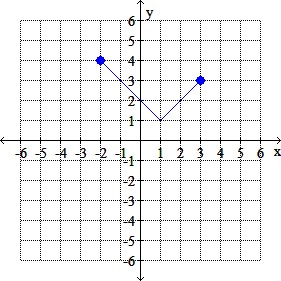
c.

d.

Question 8

Use interval notation to write the intervals over which f is   and 

Select one:

a.a. (-∞, -2)  (2, ∞)
b. never decreasing
c. (-2, 2)

b.a. (-4, ∞)
b. (-∞, -4)
c. never constant

c.a. never increasing
b. (-∞, -2)  (2, ∞)
c. (-2, 2)

d.a. (-∞, 2)  (2, ∞)
b. never decreasing
c. (-2, 2)

Question 9

Determine the minimum or maximum value of the function.

k(x) = 3x² – 4x

Select one:

a.Maximum: 4343

b.Minimum: – 4343

c.Minimum: 4343

d.Maximum: – 4343

Question 10

Graph the function and determine the minimum or maximum value of the function.

m(x) = – 1414(x + 1)²

Select one:

a.maximum value = 0

b.minimum value = 0

c.maximum value = 0

d.minimum value = 0

Question 11

p  = 3³ – 3

a. Identify the power function of the form y = x ⁿ that is the parent function to the given graph.
b. In order, outline the transformations that would be required on the graph of y = x ⁿ to make the graph of the given function.
c. Match the function with the graph.

i.

ii.

iii.

iv.

Select one:

a.a.y = x³
b. Shift y = x³ to the left 3 units. Shrink vertically by a factor of . Shift downward 3 units.
c.Graph iv.

b.a.y = x³
b. Shift y = x³ to the left 3 units. Stretch vertically by a factor of 3. Shift downward 3 units.
c.Graph i.

c.a.y = x³
b. Shift y = x³ to the left 3 units. Stretch vertically by a factor of 3. Shift downward 3 units.
c.Graph ii.

d.a.y = x³
b. Shift y = x³ to the left 3 units. Stretch vertically by a factor of 3. Shift downward 3 units.
c.Graph iii.

Question 12

Solve the problem.

f = – ⁴
a. Identify the power function of the form y = xⁿ that is the parent function to the given graph.
b. In order, outline the transformations that would be required on the graph of y = xⁿ to make the graph of the given function.
c. Match the function with the graph.

i.ii.

iii.iv.

Select one:

a.a.y = x⁴
b. Shift y = x⁴ to the right 1 units. Shrink vertically by a factor of . Reflect across the x-axis.
c.Graph ii.

b.a.y = x⁴
b. Shift y = x⁴ to the left 1 units. Shrink vertically by a factor of . Reflect across the x-axis.
c.Graph iii.

c.a.y = x⁴
b. Shift y = x⁴ to the left 1 units. Shrink vertically by a factor of .
c.Graph i.

d.a.y = x⁴
b. Shift y = x⁴ to the right 1 units. Shrink vertically by a factor of . Reflect across the x-axis.
c.Graph iii.

Question 13

Write a polynomial f (x) that meets the given conditions. Answers may vary.

Degree 3 polynomial with zeros 4, 5i, and -5i

Select one:

a.f (x) = x³ – 4x² – 25x + 100

b.f (x) = x³ + 4x² – 25x – 100

c.f (x) = x³ + 4x² + 25x + 100

d.f (x) = x³ – 4x² + 25x – 100

Question 14

Use synthetic division to divide the polynomials.

(s⁴ + 5s³ + 2s² – 17s + 7) ÷ (s – 1)

Select one:

a.s³ + 6s² + 8s – 9

b.s³ + 4s² – 2s – 15 + 22s+122s+1

c.s³ + 6s² + 8s + −9s+2s−1−9s+2s−1

d.s³ + 6s² + 8s – 9 – 2s−12s−1

Question 15

Find all the zeros.

f (x) = x³ + 10x² + 25x + 18

Select one:

a.2, -4 ± 7–√7

b.-2, -4 ± 7–√7

c.-2, -4 ± 7i

d.2, -4 ± 7i

Question 16

Find the zeros and their multiplicities. Consider using Descartes’ rule of signs and the upper and lower bound theorem to limit your search for rational zeros.

f (x) = x⁹ + 10x⁸ + 27x⁷ + 20x⁶ + 50x⁵

Select one:

a.0 (multiplicity 5), -5 (multiplicity 2) and ±i2–√2 (each multiplicity 1)

b.0 (multiplicity 5), 5 (multiplicity 2) and ±i2–√2 (each multiplicity 1)

c.0 (multiplicity 5), 5 (multiplicity 2) and ±2i (each multiplicity 1)

d.0 (multiplicity 5), 5 (multiplicity 2) and ±2–√2 (each multiplicity 1)

Question 17

A one-to-one function is given. Write an expression for the inverse function.

g (x) = r (x + q)⁷ + s

Select one:

a.g ^-1(x) = 

b.g ^-1(x) =  – q

c.g ^-1(x) = 

d.g ^-1(x) =  – q

Question 18

Provide the missing information.

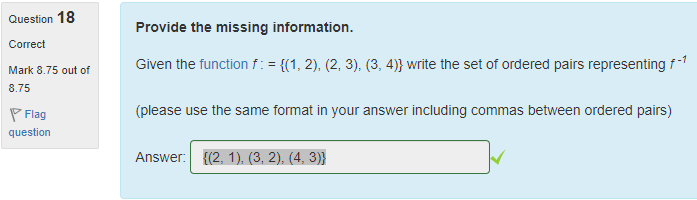
Given the function f : = {(1, 2), (2, 3), (3, 4)} write the set of ordered pairs representing f ^-1 

(please use the same format in your answer including commas between ordered pairs)

Correct Answer Question 18 

Question 19

A one-to-one function is given. Write an expression for the inverse function.

f (x) = 

Select one:

a.f ^-1(x) = 6 – 2x

b.f ^-1(x) = 

c.f ^-1(x) = 6 + 2x

d.f ^-1(x) = 

Question 20

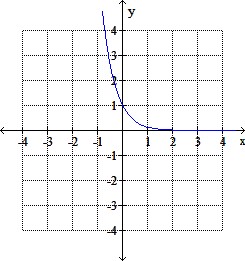
The graph of a function is given. Graph the inverse function.

Select one:

a.

b.

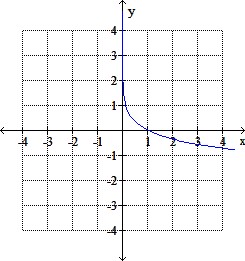
c.

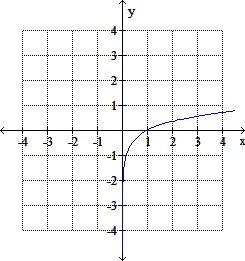
d.

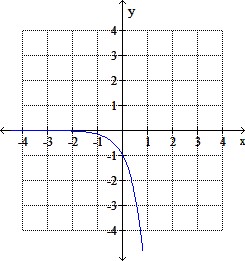
Related: (Solution) MAT101 Graded Exam 4 – Solving Linear Systems

To get all 100% correct solutions for MAT101 College Algebra Graded Exam 3

…Please click on the Icon below to purchase the FULL ANSWER at only $7

$7.00 – Purchase Checkout Added to cart