Economics 2122A Econometrics I Assignment 4

Instruction: when you make your submission, please put your answers in a single file and upload it to “Assignment” on OWL.

Question 1 (Show your steps, not only the final results.)

Based on a previous study, 43% of business graduates believe that a course in business ethics is very important for imparting ethical values to students (David, Anderson, and Lawrimore 1990). Collect a random sample of 80 business graduates. Find the probability that more than one-half of these 80 business graduates have this belief.

Question 2 (Show your steps, not only the final results.)

A business school placement director wants to estimate the mean annual salaries 5 years after students graduate. A random sample of 25 such graduates found a sample mean of $42,740 and a sample standard deviation of $4,780. Find a 90% confidence interval for the population mean, assuming that the population distribution is normal.

Question 3 (Show your steps, not only the final results.)

A college admissions officer for an MBA program has determined that historically applicants have undergraduate grade point averages that are normally distributed with standard deviation 0.45. From a random sample of 25 applications from the current year, the sample mean grade point average is 2.90. Based on these sample results, a statistician obtains a confidence interval for the population mean from 2.81 to 2.99. What is the confidence level associated with this interval?

Related: (Solution) Economics 2122A Econometrics I Assignment 5

Solution – Economics 2122A Econometrics I Assignment 4

Based on a previous study, 43% of business graduates believe that a course in business ethics is very important for imparting ethical values to students (David, Anderson, and Lawrimore 1990). Collect a random sample of 80 business graduates. Find the probability that more than one-half of these 80 business graduates have this belief.
Solution: let 𝑋 be the number of business graduates. Then 𝑋 has a binomial distribution with 𝑛=80 and 𝑃=0.43. Approximating the required probability gives the following:

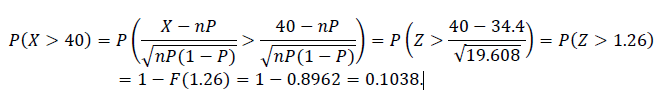
…Please click on the Icon below to purchase the full answer at only $7

$7.00 – Purchase Checkout Added to cart